서론

본 포스트에서는 다양한 대규모 DB, 클라우드 서비스에서 활용되는 Unum’s open-source Vector Search primitives를 최적화 하는 과정을 담고 있습니다. 특히 벡터 검색에서 가장 빈번하게 사용되는 **‘코사인 유사도’**에 대한 연산을 순차적으로 최적화하는 과정을 설명합니다. 결과를 미리 스포하자면 밴치마크 결과 순수 Python 코드 대비 2,500배 성능 개선을 이뤄냈습니다. 이 과정을 같이 학습해 봅시다.

각 과정은 다음 표를 참고하세요:

단계	주요 변화	누적 속도 향상
Python(기본)	순수 Python 구현	–
zip 최적화	리스트 2회 순회 → 1회	1.3×
NumPy	잘못 쓰면 35× 느려짐!	0.03×
SciPy	BLAS 호출	2–5×
C	타입별 매크로	200×
SIMD Intrinsics	AVX-512	400×
BMI2 + goto	분기 최소화	747×
AVX-512 FP16	half-precision	1,260×
AVX-512 VNNI	8-bit dot product	2,521×

코사인 유사도, 코사인 거리

우선 간단하게 **‘코사인 유사도’**와 **‘코사인 거리’**에 대해 간단하게 알아봅시다. ‘코사인 유사도’ 란, 서로 다른 두 벡터가 얼마나 비슷한 방향을 보고 있는지를 나타내는 값입니다.

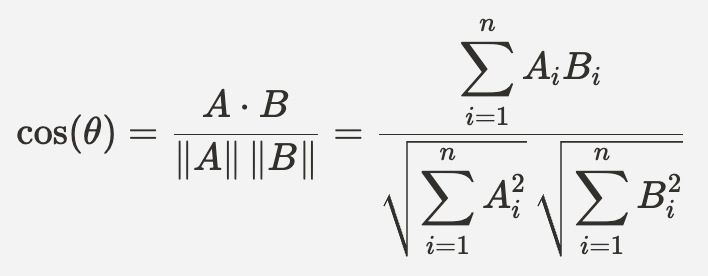
**‘코사인 유사도’**의 값은 -1 ~ 1의 범위를 가집니다.

• -1 : 두 벡터의 방향이 정 반대
• 0 : 두 벡터가 직교
• 1 : 두 벡터의 방향이 같음

**‘코사인 거리’**는 1 - 코사인 유사도로, 0 ~ 2의 범위를 가집니다.

Python

이제 ‘코사인 거리’를 순수 python으로 구현해 봅시다.

def cosine_distance(a, b):
    dot_product = sum(ai * bi for ai, bi in zip(a, b))
    magnitude_a = math.sqrt(sum(ai * ai for ai in a))
    magnitude_b = math.sqrt(sum(bi * bi for bi in b))
    cosine_similarity = dot_product / (magnitude_a * magnitude_b)
    return 1 - cosine_similarity

위 코드는 수학 공식을 그대로 코드로 변환한 결과입니다.

이제 위 코드를 4세대 Intel Xeon CPU(codenamed Sapphire Rapids)에서 실행해 보겠습니다. 이 CPU는 AWS에서 r7iz 인스턴스로 제공됩니다. 벤치마크를 실행하기 위해 난수를 생성하여 list에 넣습니다. list의 길이는 1536입니다. 이는 OpenAI Ada 서비스의 1536차원 “임베딩”을 시뮬레이션 하기 위함입니다.

np.random.seed(0)
a_list = np.random.rand(1536).tolist()
b_list = np.random.rand(1536).tolist()

%timeit 유틸리티로 벤치마크를 실행하면 루프당 93.2 µs ± 1.75 µs가 측정됩니다. 즉, 호출당 약 100 마이크로초입니다. 이 결과는 과연 좋은 걸까요, 나쁜 걸까요?

우리의 Python 코드는 파이썬답게 이해하기 쉽지만 한편으로는 비효율적인 부분이 존재합니다. a_list, b_list를 각 2번씩 순회합니다.

Zip 사용

가장 흔하게 사용되는 zip 구문을 적용해 불필요한 순회를 줄여 봅시다.

def cosine_distance(a, b):
    dot_product = 0
    magnitude_a = 0
    magnitude_b = 0
    for ai, bi in zip(a, b):
        dot_product += ai * bi
        magnitude_a += ai * ai
        magnitude_b += bi * bi
    cosine_similarity = dot_product / (math.sqrt(magnitude_a) * math.sqrt(magnitude_b))
    return 1 - cosine_similarity

이제 각 리스트를 한번씩만 순회합니다. 벤치마크 결과는 루프당 65.3 µs ± 716 ns로, 약 30 % 속도가 향상되었습니다! 꽤 좋은 결과이지만 우리는 여기서 더 최적화 방법을 찾아볼 것입니다.

Numpy : C와 Python 그 어딘가..

Numpy는 Python에서 배열을 쉽고 빠르게 다룰수 있도록 도와줍니다. 많은 개발자들이 수식 계산을 수행할 때 Numpy를 활용합니다. 또, 머신러닝 코드에서도 쉽게 찾아볼 수 있습니다. Numpy는 C로 작성되어 있으니 당연히 빠를것이라 기대하게 됩니다.

Numpy를 우리의 코드에 본격적으로 적용시키기 전에, Numpy에서 제공하는 타입인 float16, float32, int8에 대해 간단하게 정리해 보겠습니다.

구분	표준	비트 분포(부호·지수·가수)	메모리	유효 자릿수(10진수)	정규값 범위²
Half-precision(float16)	IEEE 754 half	1 · 5 · 10	16 bit (2B)	≈ 3.3	6.1 × 10⁻⁵ ~ 6.6 × 10⁴
Single-precision(float32)	IEEE 754 single	1 · 8 · 23	32 bit (4B)	≈ 7.2	1.4 × 10⁻⁴⁵ ~ 3.4 × 10³⁸
8-bit integer(int8)	2의 보수 정수	1 · 7	8 bit (1B)	정수 ±128	–128 ~ +127

이 타입들은 Meta의 FAISS나 Unum의 USearch에서 Quantization(데이터를 더 작게 만드는 것)을 수행할 때 자주 사용됩니다. 각각의 장단점을 고려해 적절하게 사용해야 합니다.

	float16	float32	int8
메모리 / 대역폭 사용량	-	x 2	x 0.25
연산량(FLOPs/레지스터)	2× ↑	-	4× ↑ (8-bit FMA)
정밀도	낮음, 누적 합 불안정	균형	정수 오버플로, 스케일 관리 필요
SW 지원 정도	개선 중	가장 안정	딥러닝 특화 라이브러리에 집중
전력 효율	좋음	보통	매우 좋음
사용 난이도	Mixed/scale 관리 필요	쉬움	스케일/제로포인트 튜닝 필요

이제 Numpy에서 제공하는 타입으로 벤치마크를 수행해 봅시다.

halfs = np.random.rand(1536).astype(np.float16)
floats = np.random.rand(1536).astype(np.float32)
ints = (np.random.rand(1536) * 100).astype(np.int8)

결과

• halfs: 525 µs ± 9.69 µs per loop.
• floats: 349 µs ± 5.71 µs per loop.
• ints: 2.31 ms ± 26 µs per loop.

위 결과를 보면 더 빨라지기는 커녕, 이전 결과인 65.3 µs보다 약 35배나 느려졌습니다. 왜일까요?

• 메모리 관리: NumPy는 C 배열을 사용합니다. 그러나, cosine_distance 함수의 내부 루프를 돌 때마다 Numpy 타입의 작은 데이터를 더 큰 Python 객체로 변환합니다. 예를 들어 float32 타입의 경우, 매 순회마다 리스트의 각 원소가 numpy.float32 PyObject 로 래핑되어 파이썬 영역으로 올라옵니다. 이 객체는 원본 데이터 뿐만 아니라 래퍼런스 카운터, 타입포인터 등 추가적인 메타데이터를 포함합니다. 이 객체가 반복적으로 생성, 소멸되며 메모리 관리 측면에서 과부하가 걸리게 됩니다.
• float16 지원: 요즘 최신의 하드웨어는 float16을 대부분 지원하지만, 소프트웨어 쪽은 그렇지 못합니다. 극소수 AI 도구만 float16를 활용하고, 대부분 GPU 중심이라 CPU 지원이 부족합니다. 따라서 float16을 지원하지 않는 경우 float16(입력) → float32(연산 수행) → float16(출력) 순서로 타입 변환이 발생합니다. 껍데기만 float16이고, 실제 연산은 float32로 수행되는 것이며, 그 과정에서 발생하는 타입 변환으로 인해 성능은 느려지게 됩니다.
• 정수 오버플로: int8로 수학 수식 계산을 수행하면 여러 문제가 발생합니다. int8이 Python int로 변환된 뒤, 연산을 수행하게 되면, 오버플로 경고가 지속적으로 발생해 CPU가 실제 계산보다 검사에 더 많은 시간을 씁니다.

따라서 NumPy를 사용하는 경우 끝까지 NumPy만 사용하는 것이 성능상 유리합니다. 순수 Python과 혼용되면 속도가 크게 떨어질 수 있습니다!

Scipy

그럼 이제 순수 Python으로 작성된 cosine_distance를 Scipy를 사용해 구현해 봅시다. Scipy는 Numpy를 베이스로 구현되었습니다. Scipy는 유용한 수학, 과학 계산 함수를 제공합니다. 당연히 cos 연산도 지원합니다! 이제 scipy.distance.spatial.cosine 의 성능을 측정해 봅시다.

• floats: 15.8 µs ± 416 ns per loop.
• halfs: 46.6 µs ± 291 ns per loop.
• ints: 12.2 µs ± 37.5 ns per loop.

이 결과에서 우리는 NumPy와 그 아래에 있는 C, Fortran, 어셈블리 기반 BLAS(Basic Linear Algebra Subroutines) 라이브러리의 진가를 확인할 수 있습니다. 이전 코드(Zip 사용)의 결과가 65.3 µs였는데, 데이터 형식에 따라 2~5배 빨라졌습니다.

이처럼 Numpy를 사용하는 경우에는 Numpy와 이를 베이스로 하는 라이브러리를 사용하는 것이 성능 측면에서 유리합니다.

C

C는 하드웨어에 독립적인 프로그래밍 언어 중 가장 저수준이어서, 코사인 유사도/거리와 같은 가벼운 연산 함수를 최적화하는데 좋은 선택입니다. 또한 C로 작성한 함수를 기본 Python 런타임의 순수 CPython 바인딩으로 감싸는 작업도 매우 간단합니다. 또한, 만약 FastCall 컨벤션을 사용하면, 커스텀 코드를 내장 Python 함수만큼 빠르게 만들 수도 있습니다. 다만, C++과 달리 C는 “제네릭”이나 “템플릿 함수”를 지원하지 않습니다. 따라서 지원하려는 각 자료형에 대해 cosine_distance 함수를 각각 구현하거나, “매크로”를 사용해야 합니다.

#define SIMSIMD_MAKE_COS(name, input_type, accumulator_type, converter)                                                \
    inline static simsimd_f32_t simsimd_##name##_##input_type##_cos(                                                   \
        simsimd_##input_type##_t const* a, simsimd_##input_type##_t const* b, simsimd_size_t n) {                      \
        simsimd_##accumulator_type##_t ab = 0, a2 = 0, b2 = 0;                                                         \
        for (simsimd_size_t i = 0; i != n; ++i) {                                                                      \
            simsimd_##accumulator_type##_t ai = converter(a[i]);                                                       \
            simsimd_##accumulator_type##_t bi = converter(b[i]);                                                       \
            ab += ai * bi;                                                                                             \
            a2 += ai * ai;                                                                                             \
            b2 += bi * bi;                                                                                             \
        }                                                                                                              \
        return ab != 0 ? 1 - ab * SIMSIMD_RSQRT(a2) * SIMSIMD_RSQRT(b2) : 1;                                           \
    }

위 코드는 SimSIMD에서 가져온 실제 코드입니다. 매크로 내부에서 1 / sqrtf(x)를 수행하는 SIMSIMD_RSQRT를 사용합니다. 또한, 타입별로 매크로에 대한 인스턴스화를 수행합니다.

이제 위 매크로에 대한 벤치마크를 수행해 봅시다.

SIMSIMD_MAKE_COS(serial, f32, f32, SIMSIMD_IDENTIFY)       // simsimd_serial_f32_cos
SIMSIMD_MAKE_COS(serial, f16, f32, SIMSIMD_UNCOMPRESS_F16) // simsimd_serial_f16_cos
SIMSIMD_MAKE_COS(serial, i8,  i32, SIMSIMD_IDENTIFY)       // simsimd_serial_i8_cos

위 매크로들은 다음 함수를 생성합니다.

• simsimd_serial_f32_cos: 32-bit float
• simsimd_serial_f16_cos: 16-bit half, 32-bit에 누적 연산
• simsimd_serial_i8_cos: 8-bit int, 32-bit에 누적 연산

Google Benchmark로 측정한 각 함수의 결과는 다음과 같습니다.

• floats: 1956 ns — Python보다 약 33배 빠름
• halfs: 1118 ns — Python보다 약 58배 빠름
• ints: 299 ns — Python보다 약 218배 빠름

훌륭한 결과지만, 이 코드는 컴파일 시점에 컴파일러가 무거운 일을 해 주어 효율적인 어셈블리를 생성한다는 가정에 의존합니다. 그러나, 잘 알려졌듯이 최신 컴파일러(e.g., GCC-12)조차 수작업 어셈블리보다 119배 느릴 수 있습니다.

Assembly

그럼 수작업으로 어셈블리 코드를 작성해서 성능을 끌어올려 봅시다.

Assembly는 하드웨어에 가장 가까운 low-level 프로그래밍 언어입니다. 이식성이 떨어지고 Human-Error가 발생하기 쉽기 때문에 작성, 유지보수가 가장 어렵지만, 가장 효율적인 코드를 만들 수 있고, AVX-512 같은 최신 하드웨어 기능을 활용할 수 있다는 점은 큰 메리트입니다. AVX-512는 512bit 레지스터를 통한 연산을 지원합니다. 따라서 한 사이클에 무려 float 16개를 병렬로 처리할 수 있습니다..! half-precision (float16)은 한번에 32개를 처리할수 있겠죠. AVX-512 자체는 단일 기능이 아니며, 다음과 같은 명령어들의 통칭 입니다:

• AVX-512F: 512-bit SIMD 명령
• AVX-512DQ: double-precision float 명령
• AVX-512BW: byte-word 명령
• AVX-512VL: vector 길이 확장
• AVX-512CD: 충돌 감지 명령
• AVX-512ER: 지수·역수 명령
• AVX-512PF: 프리페치 명령
• AVX-512VBMI: 바이트 조작 명령
• AVX-512IFMA: 정수 Fused-Multiply-Aadd 명령
• AVX-512VBMI2: 바이트 조작 명령 2
• AVX-512VNNI: 신경망 가속 명령
• AVX-512BITALG: bit 알고리즘 명령
• AVX-512VPOPCNTDQ: vector 팝카운트 명령
• AVX-5124VNNIW: 가변 정밀 워드 신경망 명령
• AVX-5124FMAPS: single-precision FMA 명령
• AVX-512VP2INTERSECT: 벡터 쌍 교집합 명령
• AVX-512BF16: bfloat16 명령
• AVX-512FP16: half-precision float 명령

본 포스트에서는 위 리스트 중 AVX-512VNNI와 AVX-512FP16에 대해 알아보겠습니다. 더 알고 싶다면 Intel 64 and IA-32 Architectures Software Developer’s Manual을 참고할 수 있지만 상당히 방대한 분량이므로 각오를 다지고 시작해야 합니다…

사실 요즘 시대에서는 실제로 순수 Assembly를 직접 작성할 필요는 없습니다. SIMD Intrinsics를 사용하면 C를 벗어나지 않고도 사실상 동일한 Assembly 명령을 작성할 수 있기 때문입니다.

__attribute__((target("avx512f,avx512vl"))) //
inline static simsimd_f32_t
simsimd_avx512_f32_cos(simsimd_f32_t const* a, simsimd_f32_t const* b, simsimd_size_t n) {
    __m512 ab_vec = _mm512_set1_ps(0);
    __m512 a2_vec = _mm512_set1_ps(0);
    __m512 b2_vec = _mm512_set1_ps(0);

    for (simsimd_size_t i = 0; i < n; i += 16) {
        __mmask16 mask = n - i >= 16 ? 0xFFFF : ((1u << (n - i)) - 1u);
        __m512 a_vec = _mm512_maskz_loadu_ps(mask, a + i);
        __m512 b_vec = _mm512_maskz_loadu_ps(mask, b + i);
        ab_vec = _mm512_fmadd_ps(a_vec, b_vec, ab_vec);
        a2_vec = _mm512_fmadd_ps(a_vec, a_vec, a2_vec);
        b2_vec = _mm512_fmadd_ps(b_vec, b_vec, b2_vec);
    }

    simsimd_f32_t ab = _mm512_reduce_add_ps(ab_vec);
    simsimd_f32_t a2 = _mm512_reduce_add_ps(a2_vec);
    simsimd_f32_t b2 = _mm512_reduce_add_ps(b2_vec);

    __m128d a2_b2 = _mm_set_pd((double)a2, (double)b2);
    __m128d rsqrts = _mm_mask_rsqrt14_pd(_mm_setzero_pd(), 0xFF, a2_b2);
    double rsqrts_array[2];
    _mm_storeu_pd(rsqrts_array, rsqrts);
    return 1 - ab * rsqrts_array[0] * rsqrts_array[1];
}

위 코드는 다음과 같이 동작합니다.

1. 하나의 for-loop가 두 벡터(a, b)를 순회하며 한 번에 최대 16개 항목을 동시에 처리합니다.
2. 벡터 끝에 도달하면 ((1u << (n - i)) - 1u) 마스크를 사용해 남은 항목을 로드합니다.
3. 벡터가 메모리 상에 정렬(aligned)되어 있음이 보장되지 않았으므로 loadu 명령을 사용합니다.
4. fmadd 명령을 이용해 a * b + c 를 한 번에 계산해 별도 덧셈을 피합니다.
5. reduce_add를 사용해 벡터 요소 전체를 더합니다. 이는 SIMD 코드는 아니지만 컴파일러가 해당 부분을 최적화해 줍니다.
6. rsqrt14 명령을 사용해 a2 와 b2의 역 제곱근을 매우 정확히 근사 계산하여 1/sqrt(a2), 1/sqrt(b2)를 구하고, LibC 호출을 피합니다.

이 코드에 대한 벤치마크 결과는 다음과 같습니다.

• floats: 118 ns — Python보다 약 553배 빠름
• halfs: 79 ns — Python보다 약 827배 빠름
• ints: 158 ns — Python보다 약 413배 빠름

드디어 성능이 세 자리 ns 영역에 들어왔습니다!

BMI2 and goto

C언어와 어셈블리어를 공부해 보면서 한번쯤은 접하게 되는 고정관념이 있습니다.

1. **goto**를 안티 패턴, 즉 좋을게 없는 패턴이라고 간주하는 것.
2. BMI2 계열 어셈블리 명령을 사용하지 않는 것.

그러나 개똥도 쓸 곳이 있는 법. goto는 low-level 코드를 최적화하거나 불필요한 분기를 피할 때 매우 유용합니다. BMI2은 bzhi, pdep, pext 등을 포함한 소형 명령 집합으로, 비트 조작에 아주 편리합니다! 이제 우리는 고정관념을 탈피하고 goto와 BMI2 계열 명령을 사용해, 이전 코드의 double-precision 연산을 single-precision 연산으로 업그레이드 시켜보겠습니다..!

__attribute__((target("avx512f,avx512vl,bmi2"))) //
inline static simsimd_f32_t
simsimd_avx512_f32_cos(simsimd_f32_t const* a, simsimd_f32_t const* b, simsimd_size_t n) {
    __m512 ab_vec = _mm512_set1_ps(0);
    __m512 a2_vec = _mm512_set1_ps(0);
    __m512 b2_vec = _mm512_set1_ps(0);
    __m512 a_vec, b_vec;

simsimd_avx512_f32_cos_cycle:
    if (n < 16) {
        __mmask16 mask = _bzhi_u32(0xFFFFFFFF, n);
        a_vec = _mm512_maskz_loadu_ps(mask, a);
        b_vec = _mm512_maskz_loadu_ps(mask, b);
        n = 0;
    } else {
        a_vec = _mm512_loadu_ps(a);
        b_vec = _mm512_loadu_ps(b);
        a += 16, b += 16, n -= 16;
    }
    ab_vec = _mm512_fmadd_ps(a_vec, b_vec, ab_vec);
    a2_vec = _mm512_fmadd_ps(a_vec, a_vec, a2_vec);
    b2_vec = _mm512_fmadd_ps(b_vec, b_vec, b2_vec);
    if (n)
        goto simsimd_avx512_f32_cos_cycle;

    simsimd_f32_t ab = _mm512_reduce_add_ps(ab_vec);
    simsimd_f32_t a2 = _mm512_reduce_add_ps(a2_vec);
    simsimd_f32_t b2 = _mm512_reduce_add_ps(b2_vec);

    // Compute the reciprocal square roots of a2 and b2
    __m128 rsqrts = _mm_rsqrt14_ps(_mm_set_ps(0.f, 0.f, a2 + 1.e-9f, b2 + 1.e-9f));
    simsimd_f32_t rsqrt_a2 = _mm_cvtss_f32(rsqrts);
    simsimd_f32_t rsqrt_b2 = _mm_cvtss_f32(_mm_shuffle_ps(rsqrts, rsqrts, _MM_SHUFFLE(0, 0, 0, 1)));
    return 1 - ab * rsqrt_a2 * rsqrt_b2;
}

single-precision float: 87.4 ns — Python보다 약 747배 빠름.

대부분이 쓸모없고 사용을 피하는 두 가지(goto, BMI2)를 사용해서 큰 성능 향상을 이뤄냈습니다. 이제 두 자리 ns 영역에 진입했습니다.

참고: BMI2 확장이 처음에는 널리 사용되지 못한 이유 중 하나는, Zen 3 이전 AMD 프로세서에서 pdep과 pext 명령의 지연(latency)이 18 사이클이었기 때문입니다. 최신 CPU에서는 3 사이클의 지연으로 처리합니다.

FP16

지금까지 사용한 모든 명령어는 Ice Lake CPU에서도 동작합니다. 이제 half-precision 연산을 하드웨어 수준에서 직접 지원하는 Intel의 최신 CPU 아키텍쳐인 Sapphire Rapids를 사용해 봅시다.

simsimd_avx512_f16_cos_cycle:
    if (n < 32) {
        __mmask32 mask = _bzhi_u32(0xFFFFFFFF, n);
        a_i16_vec = _mm512_maskz_loadu_epi16(mask, a);
        b_i16_vec = _mm512_maskz_loadu_epi16(mask, b);
        n = 0;
    } else {
        a_i16_vec = _mm512_loadu_epi16(a);
        b_i16_vec = _mm512_loadu_epi16(b);
        a += 32, b += 32, n -= 32;
    }
    ab_vec = _mm512_fmadd_ph(_mm512_castsi512_ph(a_i16_vec), _mm512_castsi512_ph(b_i16_vec), ab_vec);
    a2_vec = _mm512_fmadd_ph(_mm512_castsi512_ph(a_i16_vec), _mm512_castsi512_ph(a_i16_vec), a2_vec);
    b2_vec = _mm512_fmadd_ph(_mm512_castsi512_ph(b_i16_vec), _mm512_castsi512_ph(b_i16_vec), b2_vec);
    if (n)
        goto simsimd_avx512_f16_cos_cycle;

이전 코드와 달라진 점은 다음과 같습니다:

• 이제 half-precision을 하드웨어 수준에서 지원하므로 한 사이클(루프)당 32개를 동시에 처리합니다.
• _ps 명령어의 half-precision 버전인 _ph를 사용합니다.

half에 대한 벤치마크 결과는 51.8 ns로, Python 대비 약 1 260배 빠릅니다.

VNNI(Vector Neural Network Instructions)

오늘 살펴볼 마지막 명령어는 AVX-512VNNI의 vpdpbusd 입니다.

vpdpbusd

이 명령어는 **8-bit 정수 곱 × 누적 연산(dot product)**을 고속으로 수행합니다.

__m512i _mm512_dpbusd_epi32(__m512i acc, __m512i a, __m512i b);

• a: unsigned 8-bit int 벡터

• b: signed 8-bit int 벡터

• a × b (각 요소 쌍) → 16-bit int 결과

• 이 결과들을 4개씩 더해서 → 32-bit acc 벡터에 더함

  → 즉, (**a₀×b₀ + a₁×b₁ + a₂×b₂ + a₃×b₃)** 를 한 번에 하나의 int32로 더하는 방식

예시를 통해 더 자세하게 알아봅시다.

a = [10, 20, 30, 40,  5,  6,  7,  8, ...]  // unsigned 8-bit
b = [ 1,  2,  3,  4, -1, -2, -3, -4, ...]  // signed 8-bit

위와 같은 벡터 a, b가 vpdpbusd로 들어온 경우,

acc[0] += 10×1   + 20×2   + 30×3   + 40×4   = 10 + 40 + 90 + 160 = 300
acc[1] += 5×(-1) + 6×(-2) + 7×(-3) + 8×(-4) = -5 - 12 - 21 -  32 = -70
...(계속)...

처럼 4개씩 곱연산을 수행한 뒤, acc 벡터에 더합니다.

그런데 왜 4개씩 수행할까요? 깊게 들어가기엔 심화적이지만, 간단하게만 설명하자면 VNNI가 활용되는 딥러닝 분야에서는 NCHW, NHWC 와 같은 4D 텐서 내적 연산이 기본 구조이기 때문입니다.

4차원 텐서 구조 예시: [Batch, Channel, Height, Width]

또한, 4개씩 묶어 수행하는 것은 하드웨어 측면이나 SIMD 연산 처리에 유리하기 때문입니다. 텐서에 대한 내적 연산을 병렬적으로 처리할 때, 4개씩 묶어 처리하면 캐시/레지스터상의 메모리 배치에 유리할 것입니다. 또한, 512bit 크기를 가지는 레지스터는 최대 64개의 int8을 저장할 수 있습니다. 4개씩 묶으면 총 16개의 내적 연산이 수행될 것입니다. 이 결과를 int32로 받아 acc에 누적 연산을 수행하는 것입니다.

이제 실제로 적용된 코드를 살펴보겠습니다.

simsimd_avx512_i8_cos_cycle:
    if (n < 64) {
        __mmask64 mask = _bzhi_u64(0xFFFFFFFFFFFFFFFF, n);
        a_vec = _mm512_maskz_loadu_epi8(mask, a);
        b_vec = _mm512_maskz_loadu_epi8(mask, b);
        n = 0;
    } else {
        a_vec = _mm512_loadu_epi8(a);
        b_vec = _mm512_loadu_epi8(b);
        a += 64, b += 64, n -= 64;
    }
    ab_i32s_vec = _mm512_dpbusd_epi32(ab_i32s_vec, a_vec, b_vec);
    a2_i32s_vec = _mm512_dpbusd_epi32(a2_i32s_vec, a_vec, a_vec);
    b2_i32s_vec = _mm512_dpbusd_epi32(b2_i32s_vec, b_vec, b_vec);
    if (n)
        goto simsimd_avx512_i8_cos_cycle;

위에서 설명했던 대로 한 번의 loop에서 64개의 int8을 병렬 처리 합니다.

추가적으로, 위 코드를 컴파일 하게 되면, 컴파일러는 vpdpbusd 명령어를 추가적으로 배치합니다. 이는 if-else 분기 최적화를 위한 것으로, 분기 양쪽 모두 vpdpbusd를 중복 삽입합니다. 이는 실제 CPU에서 연산이 수행될 때 분기 지연(Predictor Miss)나 파이프라인 플러시를 줄이는 효과를 가져옵니다. 또한, AVX-512 명령어들은 내부적으로 micro-op로 작게 쪼개져 CPU 스케쥴러가 적절하게 재배치해 실행합니다.

컴파일된 코드는 다음과 같습니다.

.L2:
        ; `if (n < 64)` 검사, 참이면 L7로 점프
        cmp     rax, rdx
        je      .L7
        ; `a`와 `b`에서 64바이트 로드해 zmm1, zmm0에 저장
        vmovdqu8        zmm1, ZMMWORD PTR [rdi]
        vmovdqu8        zmm0, ZMMWORD PTR [rsi]
        ; 포인터 64바이트씩 증가
        add     rdi, 64
        add     rsi, 64
        ; 혼합 정밀도 도트 제품
        vpdpbusd        zmm4, zmm1, zmm0 ; ab = b * a
        vpdpbusd        zmm3, zmm1, zmm1 ; b2 = b * b
        vpdpbusd        zmm2, zmm0, zmm0 ; a2 = a * a
        ; 남은 항목 수 차감 후 루프 반복
        sub     rdx, 64
        jne     .L2
.L7:
        ; 꼬리 처리: 우선 k1 마스크 생성
        mov     rdx, -1
        bzhi    rax, rdx, rax
        kmovq   k1, rax
        ; k1 마스크를 적용해 64바이트 미만 로드
        vmovdqu8        zmm1{k1}{z}, ZMMWORD PTR [rdi]
        vmovdqu8        zmm0{k1}{z}, ZMMWORD PTR [rsi]
        ; 혼합 정밀도 도트 제품
        vpdpbusd        zmm3, zmm1, zmm1 ; b2 = b * b
        vpdpbusd        zmm4, zmm1, zmm0 ; ab = b * a
        vpdpbusd        zmm2, zmm0, zmm0 ; a2 = a * a
        ; 루프 종료
        jmp     .L4

컴파일러가 코드를 어떻게 수정/재배치하는지 살펴보는 일은 고통스럽긴 하지만, 흥미롭기도 합니다. 특히 짧은 코드에서 예상치 못한 결과를 접하게 될 때 더욱 그렇습니다. 사실 대규모 SIMD 명령은 micro-op로 취급되어 분해되고, CPU는 컴파일러가 제시한 순서를 무시한 채 다시 스케쥴러에서 재배열합니다.

위 코드를 Google Benchmark로 시험한 결과 ints: 25.9 ns, 최초 Python 기준보다 약 2 521배 빨랐습니다.

마치며

대규모 프로젝트, 거대한 인프라에서 제공하는 오픈소스들은 최적화가 잘 되어있는 것이 사실입니다. 그러나, 본 포스트에서 살펴본 대로 최적화 여지는 항상 존재합니다. 또한, 이러한 최적화 작업은, 대규모 인프라가 존재하지 않더라도 적은 예산으로도, 개인의 힘으로도 수행될 수 있습니다. 각 단계를 잘 이해해서 여러분도 최적화를 직접 수행해 보는 것은 어떨까요?